案例名称：学习科学计算工具，领略数学之美

育人目标：了解数学理论的价值，领略数学之美；培养严谨的职业素养，培育至臻至美的工匠精神

育人元素：工匠精神、职业素养

融入知识点：NumPy理论基础及应用

融入方式：问题导入——媒体展示——讨论思考——拓展阅读——引导总结

案例详情：

1.观看矩阵运算可视化

https://www.bilibili.com/video/BV1Qk4y1d7e1?from=search&seid=15403819054895962182

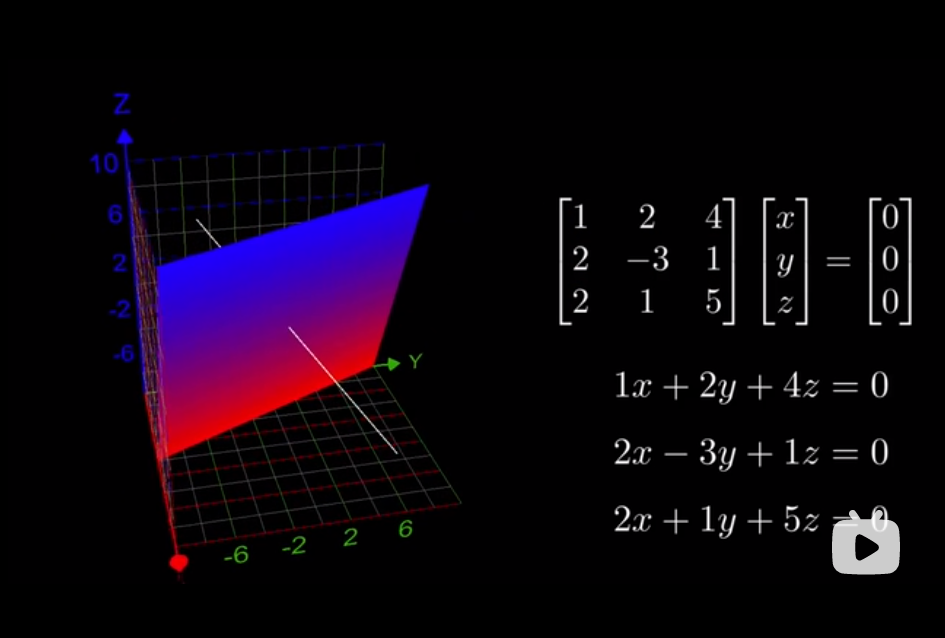
2.数学中的辩证唯物主义哲学思想

捷克数学家兼哲学家波尔达斯,德莫林斯基(Bordas-Dcmoul ins)在1898年曾说过: “没有哲学,难以得知数学的深度,当然没有数学同样也难以探知哲学的深度两者相互依存,相互依赖。”如果既无数学又无哲学,则人类就不能认识任何事物。张景中院士在《数学与哲学》书中也通过对数学发展中重大的历史事件的阐述,揭示数学与哲学的对立统一关系。此外,浏览西方数学史或哲学史,将会发现数学与哲学之间有着不解之缘,表现在:西方第一位哲学家泰勒斯是数学家；著名数学家、哲学家毕达哥拉斯是在对数学的深入研究上得出了“万物皆数”的著名哲学命题。其实,线性代数中的哲学思想处处存在,例如矩阵的可逆与不可逆,矩阵的正交与非正交,二次型的正定与非正定,向量组的相关与不相关等都体现了哲学中唯物辩证法实质与核心--对立统一规律。知识点间的对立能由此知彼,知识点间的统一能互为利用,构成了线性代数课程丰富的知识体系。再如,线性方程组进行初等行变换,其解的结构不变；矩阵进行相似变换过程,其特征值保持不变；进行合同变换过程,其正、负惯性指数不变,即人们常说的“形变神不变”亦或称之为“形变质不变”定律。总之,线性代数中的哲学思想,像一盏明灯,使我们能理清纷乱的思绪看清知识的脉络和内涵"。

案例讨论：什么是数学之美

案例升华：NumPy的学习体现了哪些工匠精神？

案例反思：我们应该以什么样的态度迎接学习的挑战。